Examen de Matemáticas CC.SS Selectividad Junio 2023 Andalucía Resuelto

©2025 Carlos Martínez Martínez

A continuación puedes ver el examen de matemáticas CC.SS de selectividad junio de 2023 Andalucía con todos los ejercicios explicados y resueltos paso a paso.

Si lo deseas, también puedes visitar mi página de exámenes de selectividad resueltos donde puedes ver exámenes de selectividad de otras convocatorias resueltos para seguir practicando.

Ejercicio 1. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

Sean la función \(F(x,y)=5x-3y\) y la región del plano definida \(R\) definida mediante las inecuaciones

$$
2x-3y\leq 1 \qquad 4x+y\leq 9 \qquad x+y \leq 5 \qquad 9x-y\geq 0 \qquad y\geq 0
$$

a) (1.3 puntos) Dibuje la región \(R\) y calcule sus vértices

La región que buscamos es,

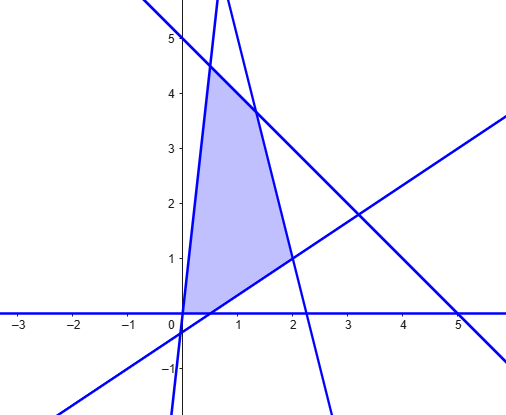
Para calcular los vértices solo tenemos que hacer la intersección entre las rectas que obtenemos a partir de las desigualdades.

$$
\left\{
\begin{align}
y &= \dfrac{2}{3}x – \dfrac{1}{3} \\
y &= -4x + 9
\end{align}
\right.
\quad \Rightarrow \quad (2,\,1)
$$

$$
\left\{
\begin{align}
y &= \dfrac{2}{3}x – \dfrac{1}{3} \\
y &= 0
\end{align}
\right.
\quad \Rightarrow \quad \left(\dfrac{1}{2},\,0\right)
$$

$$
\left\{
\begin{align}
y &= -4x + 9 \\
y &= -x + 5
\end{align}
\right.
\quad \Rightarrow \quad ( \dfrac{4}{3},\, \dfrac{11}{3} )
$$

$$
\left\{
\begin{align}
y &= -x + 5 \\
y &= 9x
\end{align}
\right.
\quad \Rightarrow \quad \left(\dfrac{1}{2},\,\dfrac{9}{2}\right)
$$

$$
\left\{
\begin{align}
y &= 9x \\
y &= 0
\end{align}
\right.
\quad \Rightarrow \quad (0,\,0)
$$

(0.5 puntos) Indique razonadamente si los puntos \(A(2,2)\) y \(B(1,3.5)\) pertenecen a la región \(R\)

Para saber si un punto pertenece a la región lo único que tenemos que hacer es verificar que cumpla las inecuaciones que definen la región. Empezamos con \(A\) y sustituimos sus coordenadas en lugar de \(x\) e \(y\)

$$
\begin{align}
2x – 3y \leq 1 &\Rightarrow 4 – 6 \leq 1 \Rightarrow \text{Verdadero} \\
4x + y \leq 9 &\Rightarrow 8 + 2 \leq 9 \Rightarrow \text{Falso}
\end{align}
$$

Por tanto ese punto no pertenece a la región, vamos a ver qué sucede con el punto \(B\)

$$
\begin{align}
2x – 3y \le 1 &\Rightarrow 2 – 10.5 \leq 1 \\
4x + y \le 9 &\Rightarrow 4 + 3.5 \leq 9 \\
x + y \le 5 &\Rightarrow 1 + 3.5 \leq 5\\
9x – y \ge 0 &\Rightarrow 9 – 3.5 \geq 0 \\
y \ge 0 &\Rightarrow 3.5 \ge 0
\end{align}
$$

Se cumplen todas las condiciones por lo que podemos afirmar que el punto \(B\) se encuentra en la región.

c) (0.7 puntos) Obtenga los puntos de la región \(R\) donde \(F\) alcanza el máximo y el mínimo y calcule sus correspondientes valores

Para calcular el máximo y el mínimo de la función en la región evaluamos la función en los vértices de la misma,

\begin{align}
&F(0,0) = 0 \\ \\
&F\left(\dfrac{1}{2},0\right) = \dfrac{5}{2} \\ \\
&F(2,1) = 7 \\ \\
&F\left(\dfrac{4}{3}, \dfrac{11}{3}\right) = -\dfrac{13}{3} \\ \\
&F\left(\dfrac{1}{2}, \dfrac{9}{2}\right) = -11
\end{align}

Por tanto afirmamos que el máximo de la función está en el vértice \((2,1)\) y vale \(7\) y el mínimo está en el punto \( \left(\dfrac{1}{2}, \dfrac{9}{2}\right) \) y vale \( -11 \)

Ejercicio 2. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

Dadas las matrices \(A =
\begin{pmatrix}
a & 1 & 0 \\
0 & a & 2 \\
0 & 1 & 1
\end{pmatrix},
\quad
B =
\begin{pmatrix}
2 & -1 \\
a & -1\
\end{pmatrix},
\quad
C =
\begin{pmatrix}
2 & -1 \\
1 & -1 \\
2 & 0
\end{pmatrix} \)

a) (1 punto) Calcule los valores del parámetro \(a\) para los que tanto \(A\) como \(B\) admiten inversa

Sabemos que una matriz tiene inversa si su determinante es distinto de cero por lo tanto,

$$
|A|=\begin{vmatrix}
a & 1 & 0 \\
0 & a & 2 \\
0 & 1 & 1
\end{vmatrix}=(a^2+0+0)-(0+2a+0)=a^2-2a=0\Leftrightarrow a=0 \quad a=2
$$

Por tanto la matriz \(A\) solo tiene inversa para valores \(a\neq 0\) y \(a\neq 2\).

Calculamos ahora el determinante de \(B\)

$$B =
\begin{vmatrix}
2 & -1 \\
a & -1
\end{vmatrix}=-2+a=0\Leftrightarrow a=2
$$

Por tanto \(B\) solo tiene inversa cuando \(a\neq 2\)

Concluimos con que \(A\) y \(B\) tienen inversa para valores \(a\neq 0\) y \(a\neq 2\)

b) (1.5 puntos) Para \(a=1\) halle una matriz \(X\) tal que \(A\cdot X \cdot B=C\)

Comenzamos despejando la ecuación matricial,

\begin{align}
&A\cdot X \cdot B=C \\
&A^{-1}\cdot A\cdot X \cdot B=A^{-1}\cdot C \\
&X\cdot B\cdot B^{-1}=A^{-1}\cdot C \cdot B^{-1}\\
&X=A^{-1}\cdot C \cdot B^{-1}
\end{align}

Calculamos las matrices inversas que necesitamos,

$$
A^{-1} =
\begin{pmatrix}
1 & 1 & -2 \\
0 & -1 & 2 \\
0 & 1 & -1
\end{pmatrix},
\qquad
B^{-1} =
\begin{pmatrix}
1 & -1\\
1 & -2
\end{pmatrix}
$$

Sustituyendo en la expresión de \(X\) obtenemos,

$$X =
\begin{pmatrix}
1 & 1 & -2\\
0 & -1 & 2\\
0 & 1 & -1
\end{pmatrix}\cdot
\begin{pmatrix}
2 & -1\\
1 & -1\\
2 & 0
\end{pmatrix} \cdot
\begin{pmatrix}
1 & -1\\
1 & -2
\end{pmatrix}=
\begin{pmatrix}
-3 & 5\\
4 & -5\\
-2 & 3
\end{pmatrix}
$$

Ejercicio 3. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

Se considera la función \(f(x)=x^3-3x^2+2x\)

a) (1 punto) Halle los puntos de corte con los ejes, los intervalos de crecimiento y decrecimiento, los extremos relativos de \(f\) y su curvatura.

Comenzamos calculando los puntos de corte con los ejes. Para el eje \(x\) sabemos que los puntos de corte coinciden con las raíces del polinomio por lo que por Ruffini podemos factorizarlo y expresar la función como,

$$
f(x)=x^3-3x^2+2x=x(x-1)(x-2)
$$

Por tanto las raíces son \(x=0,\, x=1\, x=2\) y los puntos de corte serían,

$$
(0,0),\ (1,0),\ (2,0)
$$

Con el eje \(y\) hacemos \(x=0\) y obtenemos nuevamente el punto \((0,0)\).

Pasamos a estudiar los intervalos de crecimiento y decrecimiento de la función.

Calculamos la primera derivada e igualamos a cero para obtener los candidatos a extremos relativos.

$$
f'(x)=3x^{2}-6x+2=0\Leftrightarrow 3x^{2}-6x+2=0 \quad\Longrightarrow\quad x=\frac{6\pm\sqrt{36-24}}{6}=1\pm\frac{1}{\sqrt{3}}
$$

A continuación evaluamos el signo de \(f'(x)\) en los intervalos que generan los candidatos a puntos críticos.

\begin{align}
&f'(x)>0\quad\text{en}\quad(-\infty,\;1-\dfrac{1}{\sqrt{3}})\ \cup\ (1+\dfrac{1}{\sqrt{3}},\infty)
\quad\Longrightarrow\ f\ \text{crece en esos intervalos},\\
&f'(x)<0\quad\text{en}\quad\big(1-\dfrac{1}{\sqrt{3}},\;1+\dfrac{1}{\sqrt{3}}\big)
\quad\Longrightarrow\ f\ \text{decrece en ese intervalo}.
\end{align}

Una vez hecho el estudio del crecimiento y el decrecimiento, podemos evaluar la función en los puntos que serán máximo y mínimo y obtener que,

$$
f\Big(1-\frac{1}{\sqrt{3}}\Big)=\frac{2\sqrt{3}}{9},\qquad
f\Big(1+\frac{1}{\sqrt{3}}\Big)=-\frac{2\sqrt{3}}{9}.
$$
Por tanto, \(f\) tiene un máximo relativo en \(\Big(1-\frac{1}{\sqrt{3}},\ \frac{2\sqrt{3}}{9}\Big)\).
Y \(f\) tiene un mínimo relativo en \(\Big(1+\frac{1}{\sqrt{3}},\ -\frac{2\sqrt{3}}{9}\Big)\).

Pasamos a estudiar la curvatura,

Veamos donde la segunda derivada se anula,

$$
f»(x)=6x-6=0\Leftrightarrow x=1
$$

Estudiamos el signo de la segunda derivada en los intervalos \( (-\infty, 1)\) y \((1,+\infty) \)

En \( (-\infty, 1)\), \(f»(x)<0\) por lo que \(f\) es cóncava

En \((1,+\infty) \), \(f»(x)>0\)por lo que \(f\) es convexa

b) (0.5 puntos) Represente gráficamente la función \(f\)

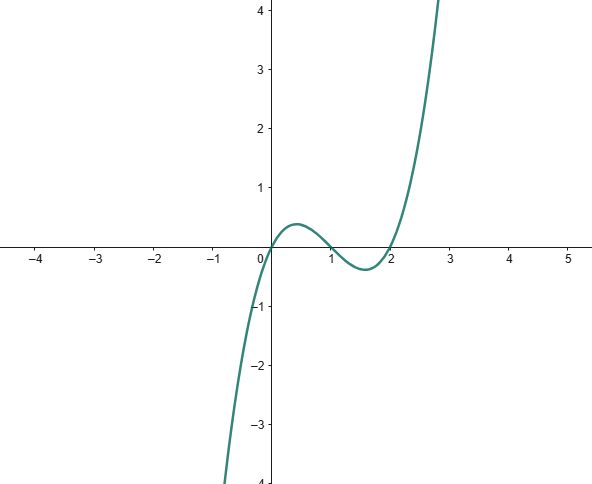
c) (1 punto) Calcula el área del recinto acotado, limitado por la gráfica de \(f\) y el eje de abscisas.

El área buscada se calcula resolviendo,

$$
\int_{0}^{1}f(x)\,dx+\int_{1}^{2}-f(x)\,dx.=\int_{0}^{1}f(x)\,dx-\int_{1}^{2}f(x)\,dx.
$$

Resolviendo cada integral tenemos,

\begin{align}
\int_{0}^{1}f(x)\,dx &=\Big[\frac{x^{4}}{4}-x^{3}+x^{2}\Big]_0^{1} = \left(\frac{1}{4}-1+1\right)-0=\frac{1}{4}, \\
\int_{1}^{2}f(x)\,dx &=\Big[\frac{x^{4}}{4}-x^{3}+x^{2}\Big]_1^{2}
= \left(\frac{16}{4}-8+4\right)-\left(\frac{1}{4}-1+1\right)
= (4-8+4)-\frac{1}{4}=-\frac{1}{4}.
\end{align}

Por lo que el área del recinto encerrado es de,

$$
\int_{0}^{1}f(x)\,dx-\int_{1}^{2}f(x)\,dx=\frac{1}{4}-\big(-\dfrac{1}{4}\big)=\frac{1}{2} \,u^2
$$

Ejercicio 4. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

Se desea analizar el valor de las acciones de una empresa en un día. La función \(v(t)\) nos indica el valor, en euros, de cada acción de la empresa en función del tiempo \(t\), medido en horas, a partir de la hora de apertura del mercado. De la función \(v(t)\) se conoce que su variación instantánea es
$$
v'(t)=t^2-5t+6 \quad t\in [0,6]
$$

a) (0.75 puntos) Determine los intervalos de crecimiento y decrecimiento de la función \(v\)

Veamos los puntos donde la derivada se anula,

$$
v'(t)=0\Leftrightarrow t^2-5t+6=0\Leftrightarrow t=\dfrac{5\pm \sqrt{25-24}}{2}\Leftrightarrow t=2\, , \, t=3
$$

Estudiamos el signo de la derivada,

\begin{array}{| c | c |c| c|}\hline & (0,2) & (2,3) & (3,6) \\
\hline \text{Signo } v'(x) & + & –& + \\
\hline v & \text{Estrictamente creciente} & \text{Estrictamente decreciente}& \text{Estrictamente creciente} \\
\hline\end{array}

b) (0.75 puntos) Si en el momento de apertura del mercado se conoce que \(v(0)=10\), halle la función \(v\)

Calculamos la función \(v\) a partir de la derivada simplemente aplicando integración,

$$
v(t)=\int (t^{2}-5t+6)\,dt
= \dfrac{t^{3}}{3}-\dfrac{5t^{2}}{2}+6t+C,
$$

A continuación imponemos la condición del enunciado para obtener el valor de la constante de integración.

$$
v(0)=10 \Rightarrow\dfrac{0^{3}}{3}-\dfrac{5\cdot 0^{2}}{2}+6\cdot 0+C=10\Leftrightarrow C=10
$$

La función buscada es \( v(t)=\dfrac{t^{3}}{3}-\dfrac{5t^{2}}{2}+6t+10\)

c) (0.5 puntos) Si un inversor compró 3000 de estas acciones en el instante \(t=2\) y posteriormente las vendió en el instante \(t=4\), indique a cuanto ascendió la ganancia o pérdida que obtuvo el inversor con esta gestión.

Si compró 3000 acciones en \(t=2\) podemos saber que el valor de la acción en dicho momento fue de
$$v(2)=\dfrac{2^{3}}{3}-\dfrac{5(2)^{2}}{2}+6(2)+10=\dfrac{44}{3}$$

Por otra parte las vendió en \(t=4\) por lo que el valor de la acción en dicho momento fue de,

$$
v(4)=\dfrac{4^{3}}{3}-\dfrac{5(4)^{2}}{2}+6(4)+10=\dfrac{46}{3}
$$

Si calculamos \( v(4)-v(2)=\dfrac{2}{3}\) tenemos la ganancia por cada acción. Multiplicando por las 3000 acciones que compró y vendió se obtiene un beneficio de 2000€.

d) (0.5 puntos) ¿En qué momentos debería este inversor haber realizado las gestiones de compra y de venta para que la ganancia hubiese sido máxima? Justifique la respuesta

Del primer apartado deducimos que en \(t=2\) existe un máximo relativo de la función y en \(t=3\) un mínimo de la función. Sabemos que al estar definida en un intervalo cerrado la función alcanza sus máximos o sus mínimos en los extremos relativos o en los extremos del intervalo de definición. Como es lógico, el máximo beneficio se obtiene cuando se compran las acciones en su valor mínimo y se venden en su valor máximo. Veamos cuanto es ese valor,

\begin{align}
&v(0)=10 \\
&v(2)=\dfrac{44}{3} \\
&v(3)=\dfrac{29}{2} \\
&v(6)= 28
\end{align}

Por lo tanto el inversor debería comprar la acción en \(t=0\) y venderla en \(t=6\) para obtener un beneficio por acción de 18€.

Ejercicio 5. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

Disponemos de una moneda trucada en la que la probabilidad de obtener cara, al lanzarla, es el doble de la de obtener cruz.

a) (0.5 puntos) Halle la probabilidad de que, al lanzar la moneda, se obtenga cara.

Comenzamos definiendo los sucesos del problema,

C=»Obtener cara al lanzar la moneda» y X=»Obtener cruz al lanzar la moneda»

Es claro que \(P(C)=\dfrac{2}{3}\)

b) (0.75 puntos) Halle la probabilidad de que, al lanzar la moneda dos veces la moneda, se obtenga una cara y una cruz sin importar el orden.

Aquí podemos plantear un diagrama de árbol ya que tenemos dos lanzamientos,

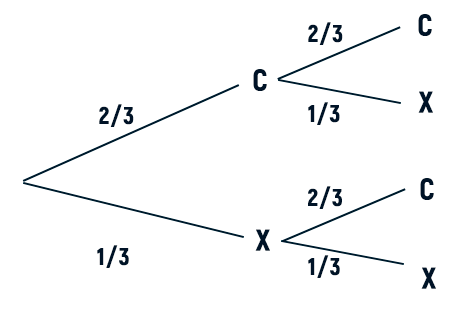
$$
P(C1)\cdot P(X2/C1)+P(X1)\cdot P(C2/X1)=\dfrac{2}{3}\cdot \dfrac{1}{3}+\dfrac{1}{3}\cdot \dfrac{2}{3}=\dfrac{4}{9}
$$

c) (0.5 puntos) Halle la probabilidad de que al lanzar dos veces la moneda se obtenga al menos una cara

En este caso lo mas sencillo es calcular la probabilidad de no obtener ninguna cara y quedarnos con el complementario

$$
P(X1)\cdot P(X2/X1)=\dfrac{1}{3}\cdot \dfrac{1}{3}=\dfrac{1}{9}
$$

Por tanto la probabilidad pedida es

$$
P(\text{al menos una cara})=1-\dfrac{1}{9}=\dfrac{8}{9}
$$

d) (0.75 puntos) Si al lanzar la moneda dos veces observamos que ha salido al menos una cara halle la probabilidad de que obtengan dos caras.

Vamos a definir nuevos sucesos para escribir correctamente el cálculo de probabilidades.

A=»Lanzar la moneda dos veces y observar que ha salido al menos una cara»

B=»Obtener dos caras»

Haciendo esta definición es claro que lo que nos piden es calcular \(P(B/A)\). Aplicando la definición de probabilidad y teniendo en cuenta que la probabilidad del suceso \(A\) la hemos calculado en el apartado anterior tenemos,

$$
P(B/A)=\dfrac{P(B\cap A)}{P(A)}=\dfrac{\dfrac{2}{3}\cdot \dfrac{2}{3}}{\dfrac{8}{9}}=\dfrac{1}{2}=0’5
$$

Ejercicio 6. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

En una base de datos de correos electrónicos se ha observado que el 20% de los correos recibidos son spam. Además, se ha observado que la palabra «lottery» ha aparecido en el 40% de los correos que son spam y en el 0.6% de los correos que no lo son.

a) (1.25 puntos) Halle la probabilidad de que en un correo elegido al azar en el que aparezca la palabra «lottery» sea spam.

Comenzamos definiendo los sucesos asociados al problema, S=´´Ser spam´´ y L=´´Contener la palabra lottery´´. Por el enunciado tenemos que

\begin{align}
&P(S)=0’2 \Rightarrow P(\overline{S})=0’8 \\
& P(L/S)=0’4 \\
& P(L/\overline{S})=0’006
\end{align}

Por otra parte podemos montar un diagrama de árbol,

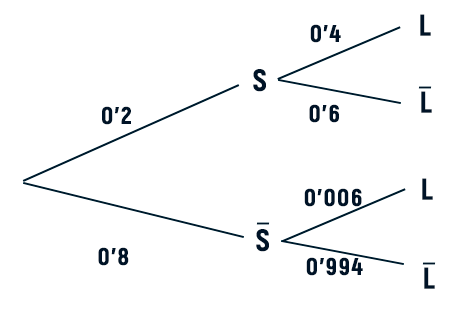
Nos piden calcular \( P(S/L)\)

Aplicando la definición de probabilidad condicionada tenemos,
$$
P(S/L)=\dfrac{P(S\cap L)}{P(L)}=\dfrac{P(S)\cdot P(L/S)}{P(S)\cdot P(L/S)+P(\overline{S})\cdot P(L/\overline{S})}=\dfrac{0’2\cdot 0’4}{0’2\cdot 0’4+0’8\cdot 0’006}=0’943
$$

b) (0.5 puntos) Halle la probabilidad de que en un correo elegido al azar en el que no aparezca la palabra lottery no sea spam.

Nos piden \( P(\overline{S}/\overline{L})\)

$$
P(\overline{S}/\overline{L})=\dfrac{P(\overline{S}\cap \overline{L}}{P(\overline{L})}=\dfrac{0’8\cdot 0’994}{0’2\cdot 0’6+0’8\cdot 0’994}=0’868
$$

c) (0.75 puntos) Si un correo se etiqueta como spam si aparece la palabra lottery y como no spam si esta palabra no aparece, calcule la probabilidad de que un correo se etiquete incorrectamente.

Etiquetar un correo incorrectamente es equivalente a calcular,

$$
P(S)\cdot P(S/\overline{L})+P(\overline{S})\cdot P(L/\overline{S})=0’2\cdot 0’6+0’8\cdot 0’006=0’124
$$

Ejercicio 7. Examen de matemáticas CC.SS selectividad Junio 2022 Andalucía

(1.25 puntos) Una población está dividida en cuatro estratos 250, 300, 400 y 350 individuos. Realizando un muestreo aleatorio estratificado con afijación proporcional se han seleccionado 20 individuos del primer estado. Determine el tamaño de la población, el tamaño de la muestra y el número de individuos seleccionados de los tres restantes estratos.

Sabemos por la teoría de muestras que cuando se da un muestreo aleatorio estratificado con afijación proporcional se ha de verificar que,

$$
\dfrac{n}{N}=\dfrac{n_1}{N_1}=\dfrac{n_2}{N_2}=\dfrac{n_3}{N_3}=\dfrac{n_4}{N_4}
$$

Por los datos que nos dan tenemos que, \(N=250+300+400+350=1300\) individuos. Además, \(n_1=20\) por tanto en particular se ha de cumplir que,

$$
\dfrac{n}{1300}=\dfrac{20}{300}
$$

De donde obtenemos que \(n=104\) individuos.

Vamos a ir trabajando la igualdad anterior para calcular el resto de valores. En el segundo estrato tendríamos,

$$
\dfrac{20}{250}=\dfrac{n_2}{300}\Rightarrow n_2=24
$$

Para el estrato número tres se tendría,

$$
\dfrac{20}{250}=\dfrac{n_3}{000}\Rightarrow n_3=32
$$

Y para el último estrato,

$$
\dfrac{20}{250}=\dfrac{n_4}{350}\Rightarrow n_4=28
$$

b) En un centro de enseñanza la calificación media de los estudiantes fue de 6.4 puntos con una desviación típica de 0.7 puntos. Se seleccionó aleatoriamente una muestra de 49 estudiantes.

b1) (0.25 puntos) Indique la distribución que sigue la media de las muestra de tamaño 49.

Sabemos que la distribución de la media muestral es \( N\big( \mu, \dfrac{\sigma}{\sqrt{n}}\big)=N\big( 6.4, \dfrac{0.7}{\sqrt{49}}\big)=N\big( 6.4, 0.1\big)\)

b2) Calcule la probabilidad de que la media de las calificaciones de los estudiantes de una de esas muestras esté comprendida entre 6.3 y 6.8 puntos.

Usando que \(Z\) es una distribución normal tipificada y consultado la tabla de probabilidades de dicha distribución podemos calcular,

\begin{align}
P(6.3 < \bar X < 6.8)&=P\left(\frac{6.3 – 6.4}{0.1}<\dfrac{\bar X-6.4}{0.1}<\frac{6.8 – 6.4}{0.1}\right)=P(-1 < Z < 4)\\ &=P(Z<4)-P(Z<1)=0.99997-(1-0.8413) \\
&=0.99997-0.1587=0.84127
\end{align}

Ejercicio 8. Examen de matemáticas CC.SS selectividad Junio 2023 Andalucía

Se desea estimar la proporción de donantes de sangre en una universidad. Para ello se toma una muestra aleatoria de 400 personas de esa universidad, resultando que 64 son donantes de sangre.

a) (1.25 puntos) Calcule un intervalo de confianza, con un nivel del 98%, para estimar la proporción poblacional de donantes de sangre.

Sabemos que el intervalo de confianza para la proporción de donantes de sangre viene dado por,

$$
\left( p-z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}, p+z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} \right)
$$

Donde \(p\) es la proporción de donantes de la muestra, \(p=64/400=0’16 \)

Sabemos que el nivel de confianza exigido es del 98% por lo que,

$$
0’98=1-\alpha\Rightarrow \alpha=0’02
$$

A continuación buscamos un valor \(z_{\alpha/2}\) que verifique

$$
P(Z < z_{\alpha/2})=1-\frac{\alpha}{2}=0’99
$$

Donde obtenemos \(z_{\alpha/2}=2’325\).

Sustituyendo ahora en la expresión del intervalo de confianza tenemos,

\begin{align}
IC&= \left( 0’16-2’325\sqrt{\frac{0’16(1-0’16)}{400}}, 0’16+2’325\sqrt{\frac{0’16(1-0’16)}{400}} \right) \\
&= \left( 0’1174,0’2026 \right) \end{align}

b) (1.25 puntos) Si el nivel de confianza es del 95%, calcule el error máximo cometido. Razone si este error será mayor o menos al disminuir el nivel de confianza

Sabemos que el error viene dado por,

$$
E=z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}
$$

Dado que el nivel de confianza es distinto calculamos,

$$
0’95=1-\alpha\Rightarrow \alpha=0’05
$$

$$
P(Z < z_{\alpha/2})=1-\frac{\alpha}{2}=0’975
$$

Obtenemos que \(z_{\alpha/2}=1’96\).

Sustituyendo en la expresión del error se tiene que,

$$
E=z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}=1’96\sqrt{\frac{0’16(1-0’16)}{400}}=0’035=3’5%
$$

Al disminuir el nivel de confianza obtenemos un valor de \(z_{\alpha/2}\) menor por lo que el error máximo cometido también disminuye.

Si quieres seguir practicando ejercicios de intervalos de confianza tanto para la media como para la proporción te dejo esta entrada con ejercicios de intervalos de confianza resueltos selectividad

Esta es una resolución particular de todos los ejercicios del examen de matemáticas CC.SS de la convocatoria de selectividad de Junio de 2023 en Andalucía (Pevau) por lo que otras soluciones planteadas también pueden ser válidas. Si te ha gustado este contenido, compártelo y no olvides visitar el resto de exámenes de selectividad de Andalucía resueltos

Si te ha gustado esta entrada con la resolución del examen de matemáticas CC.SS selectividad y quieres descubrir más material gratuito puedes visitar mi blog de matemáticas. Si te gustaría aprender más sobre matemáticas o estadística puedes visitar mi canal de Youtube donde encontrarás ejercicios resueltos de matemáticas y estadística a todos los niveles.