Examen de Matemáticas II Selectividad Junio 2023 Andalucía Resuelto

©2023 Carlos Martínez Martínez

A continuación podrás ver una solución del Examen de matemáticas II selectividad Junio 2023 Andalucía resuelto paso a paso. Si quieres ver más exámenes resueltos paso a paso para seguir preparando tu prueba de selectividad te invito a que visites mi página de exámenes de selectividad de Andalucía.

Ejercicio 1. Examen de matemáticas II selectividad junio 2023 Andalucía

Considera la función \( f : \mathbb{R} \rightarrow \mathbb{R} \) definida por \( f(x) = \frac{1}{e^x + e^{-x}} \)

a) (1.5 puntos) Estudia y halla los máximos y mínimos absolutos de \( f \) (abscisas donde se obtienen y valores que se alcanzan).

Para calcular los máximos y los mínimos absolutos de la función dada comenzamos calculando la derivada,

$$
f'(x) = \frac{- (e^x – e^{-x})}{(e^x + e^{-x})^2}.
$$

Igualando a cero calculamos los puntos críticos y candidatos a extremos relativos.

$$
f'(x)=0\Leftrightarrow \frac{- (e^x – e^{-x})}{(e^x + e^{-x})^2}=0 \Leftrightarrow e^x – e^{-x}=0
$$

Esto ocurre cuando \( e^x = e^{-x} \), lo que implica que \( x = 0 \).

Por tanto hay un candidato a extremo en \(x=0\). Estudiamos el signo de la derivada a ambos lados para saber de que se trata,
\begin{array}{| c | c |c|}\hline & (-\infty,0) & (0,\infty) \\
\hline \text{Signo } f'(x) & + & – \\
\hline f & \text{Estrictamente creciente} & \text{Estrictamente decreciente} \\
\hline\end{array}

Por tanto, evaluando el valor de la función en dicho punto \(f(0) = \frac{1}{e^0 + e^0} = \frac{1}{2}\) obtenemos que la función tiene un máximo absoluto en \((0,1/2)\)

Finalmente podemos ver que existe una asíntota horizontal ya que,

$$
\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{1}{e^x + e^{-x}}=0
$$

$$
\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{1}{e^x + e^{-x}}=0
$$

Así que la función tiene una asíntota horizontal en \(y=0\) y no tiene mínimos.

b) Calcula \( \displaystyle\lim_{x \to +\infty} x^2 f(x)\)

Comenzamos sustituyendo el valor de la función en el límite que nos plantean.

$$
\lim_{x \to +\infty} x^2 f(x) = \lim_{x \to +\infty} \frac{x^2}{e^x + e^{-x}}=\frac{\infty}{\infty}
$$

Tenemos una indeterminación de tipo \(\frac{\infty}{\infty}\), por lo que podemos que aplicar la regla de L’Hôpital para resolver el límite.

$$
\lim_{x \to +\infty} \frac{x^2}{e^x + e^{-x}}= \lim_{x \to +\infty} \frac{2x}{e^x – e^{-x}}=\frac{\infty}{\infty}
$$

De nuevo tenemos una indeterminación por lo que volvemos a aplicar la regla de L’Hôpital,

$$
\lim_{x \to +\infty} \frac{2x}{e^x – e^{-x}}= \lim_{x \to +\infty} \frac{2}{e^x + e^{-x}}=\frac{2}{+\infty} = 0
$$

Ejercicio 2. Examen de matemáticas II selectividad Junio 2023 Andalucía

Sea la función \( f : [-2, 2] \to \mathbb{R} \), definida por \( f(x) = x^3 – 2x + 5 \)

a) (1.5 puntos) Determina las abscisas de los puntos, si existen, en los que la pendiente de la recta tangente coincide con la pendiente de la recta que pasa por los puntos \( (-2, f(-2)) \) y \( (2, f(2)) \).

Comenzamos calculando la pendiente de la recta tangente que pasa por los puntos dados,

\begin{align}
f(-2)=(-2)^3-2(-2)+5=-8+4+5=1 \Rightarrow A=(-2,1) \\ \\
f(2)=2^3-2\cdot 2 +5=8-4+=9 \Rightarrow B=(2,9)
\end{align}

Como la recta tangente pasa por los puntos \(A\) y \(B\) podemos obtener el vector director de la recta como,

$$
\overrightarrow{v}=\overrightarrow{AB}=B-A=(4,8)
$$

Dado el vector director de la recta sabemos que la pendiente se obtiene como,

$$
m=\frac{8}{4}=2
$$

A continuación lo que tenemos que hacer es buscar los puntos \(x_0\) en los que la pendiente de la recta tangente coincide con 2. Dado que en la expresión general de la recta tangente la pendiente viene dada por el término \(f'(x_0)\) tenemos que imponer que \(f'(x_0)=2\)

$$
f'(x)=3x^2-2\Rightarrow f'(x_0)=3x_0^2-2=2\Rightarrow x_0^2=\frac{4}{3}\Rightarrow x_0=\pm \frac{2}{\sqrt{3}}
$$

Y así hemos obtenido los puntos de abscisas que nos pedían.

b) (1 punto) Determina la ecuación de la recta tangente y la ecuación de la recta normal a la gráfica de \( f \) en el punto de inflexión

Buscamos el punto de inflexión imponiendo la nulidad de la segunda derivada

$$
f^″(x)=6x=0\Leftrightarrow x=0
$$

La recta tangente en \(x=0\) viene dada por

\begin{align}
&y-f(0)=f'(0)(x-0) \\
&y-5=-2(x-0) \\
&y=-2x+5
\end{align}

Por otra parte la ecuación de la recta normal viene dada por,

$$
y-5=\frac{1}{2}(x-0) \\
y=\frac{1}{2}x+5
$$

Ejercicio 3. Examen de matemáticas II selectividad Julio 2023 Andalucía

Considera la función \( f : \mathbb{R} \to \mathbb{R} \), definida por \( f(x) = x|x – 1| \). Calcula el área del recinto limitado por la gráfica de dicha función y su recta tangente en el punto de abscisa \( x = 0 \).

Comenzamos expresando la función valor absoluto como una función definida a trozos,

$$
f(x) =
\begin{cases}
-x(x-1)=-x^2+x, & \text{si } x < 1 \\
x(x – 1)=x^2-x, & \text{si } x \geq 1
\end{cases}
$$

Calculamos la recta tangente de la función en el punto \(x=0\).

$$
y-f(0)=f'(x)(x-0)
$$

La expresión de la derivada viene dada por,

$$
f'(x) =
\begin{cases}
-2x + 1, & \text{si } x < 1
2x – 1, & \text{si } x > 1
\end{cases}
$$

Así la expresión de la recta tangente es,

$$
y-0=1(x-0)\Rightarrow y=x
$$

Las función junto con la recta tangente se puede representar como,

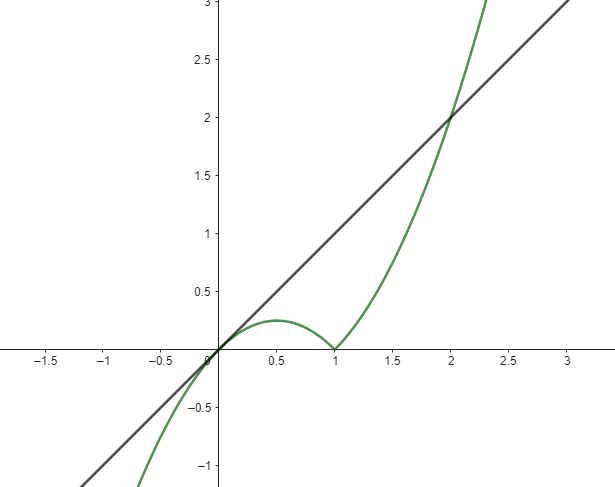
Calculando los puntos de corte obtenemos \(x=0\) y \(x=2\) como intersección de la función y la recta tangente. El área del recinto limitado se obtiene resolviendo la siguiente integral

\begin{align}
&\int_0^1 \left( x – (-x^2 + x) \right) \, dx + \int_1^2 \left( x – (x^2 – x) \right) dx \\ \\
&\int_0^1x^2dx+\int_1^2-x^2+2x dx \\ \\
&\left[\frac{x^3}{3}\right]_0^1+\left[ -\frac{x^3}{3}+x^2\right]_1^2 \\ \\
&\frac{1}{3}+ \left( -\frac{8}{3}+4\right)-\left( -\frac{1}{3}+1\right)=1 u^2
\end{align}

Ejercicio 4. Examen de matemáticas II selectividad Junio 2023 Andalucía

Considera la función \( F : \mathbb{R} \to \mathbb{R} \) definida por \(F(x) = \displaystyle\int_0^x \sin\left(t^2\right) dt\). Calcula \(\displaystyle\lim_{x \to 0} \frac{x F(x)}{\sin(x^2)}\)

Para resolver este límite debemos tener en cuenta el teorema fundamental del cálculo integral en el que se relacionan integral y derivada de manera que

$$
F'(x)=f(x) \Rightarrow F'(x)=\sin(x^2) \Rightarrow F^″(x)=2x\cos(x^2)
$$

Ahora planteamos la resolución del límite,

\begin{align}
&\displaystyle\lim_{x \to 0} \frac{x F(x)}{\sin(x^2)}=\frac{0\cdot F(0)}{\sin(0^2)}=\frac{0}{0}\text{ Aplicamos L’Hôpital} \\ \\
& \displaystyle\lim_{x \to 0} \frac{F(x)+xF'(x)}{2x\cos(x^2)}=\frac{F(0)+0F'(0)}{2\cdot 0\cos(0)}=\frac{0}{0}\text{ Aplicamos L’Hôpital} \\ \\
&\displaystyle\lim_{x \to 0}\frac{F'(x)+F'(x)+xF^″(x)}{2\cos(x^2)-(2x)^2\sin(x^2)}=\frac{F'(0)+F'(0)+0F^″(0)}{2\cos(0^2)-(2\cdot 0)^2\sin(0^2)}=\frac{0}{2}=0
\end{align}

Ejercicio 5. Examen de matemáticas II selectividad Junio 2023 Andalucía

Una marca de vehículos ha vendido este mes coches de tres colores: blancos, negros y rojos. El 60% de los coches blancos más el 50% de los coches negros representan el 30% de los coches vendidos. El 20% de los coches blancos junto con el 60% de los coches negros y el 60% de los coches rojos representan la mitad de los coches vendidos. Se han vendido 100 coches negros más que blancos. Determina el número de coches vendidos de cada color.

Comenzamos definiendo las variables del problema,

\begin{align}
&x=\text{número de coches blancos} \\
&y=\text{número de coches negros} \\
&z=\text{número de coches rojos}
\end{align}

El sistema de ecuaciones planteado a partir del enunciado del problema es

$$\left\{
\begin{align}
0.6x+0.5y&=0.3(x+y+z)\\
0.2x+0.6y+0.6z&=0.5(x+y+z)\\
y&=x+100
\end{align} \right.$$

Podemos multiplicar las dos primeras igualdades por 10 para obtener un sistema equivalente que sea más fácil de trabajar,

$$\left\{
\begin{align}
6x+5y&=3(x+y+z)\\
2x+6y+6z&=5(x+y+z)\\
y&=x+100
\end{align} \right.$$

Desarrollando los productos podemos obtener el siguiente sistema equivalente que podremos resolver,

$$\left\{
\begin{align}
3x+2y-3z&=0\\
-3x+y+z&=0\\
-x+y&=100
\end{align} \right.$$

Este sistema se puede resolver por Gauss, por Cramer o sustituyendo de abajo hacia arriba. Tomando esta última opción obtenemos,

$$\left\{
\begin{align}
3x+2(100+x)-3z=0\\
-3x+100+x+z=0
\end{align} \right.$$
$$
\left\{
\begin{align}
5x-3z=-200\\
-2x+z=-100
\end{align} \right.
$$

Resolviendo obtenemos \(x=500\), \(y=600\) y \(z=900\)

Ejercicio 6. Examen de matemáticas II selectividad Junio 2023 Andalucía

Considera las matrices \(
A =
\begin{pmatrix}
0 & 0 & m \\
m & 0 & 0 \\
0 & m & 0
\end{pmatrix},
\quad
B =
\begin{pmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{pmatrix}
\)

a) (0.5 puntos) Determina para qué valores de \(m\) existe la matriz inversa de \(A\)

Calculamos el determinantes y vemos para qué valores se anula

$$
|A| =
\begin{vmatrix}
0 & 0 & m \\
m & 0 & 0 \\
0 & m & 0
\end{vmatrix}
=(0+m^3+0)-(0+0+0)=0\Leftrightarrow m=0
$$

Por tanto existe la matriz inversa para valores de \(m\neq 0\)

b) (2 puntos) Para todo \( m \neq -1 \), resuelve, si es posible, la ecuación \( AX + X = B \)

Resolvemos la ecuación matricial de forma teórica sin sustituir las matrices,

\begin{align}
AX+X&=B \\
(A+I)X&=B \\
X&=(A+I)^{-1}\cdot B
\end{align}

Calculamos entonces las matrices que necesitamos,

$$
(A+I)^{-1}=\dfrac{Adj((A+I))^t}{|(A+I)|}
$$

Calculamos el determinante,

$$
|A+I| =
\begin{vmatrix}
1 & 0 & m \\
m & 1 & 0 \\
0 & m & 1
\end{vmatrix}
=(1+m^3+0)-(0+0+0)=m^3+1
$$

$$
(A+I)^t =
\begin{pmatrix}
1 & m & 0 \\
0 & 1 & m \\
m & 0 & 1
\end{pmatrix}
$$

$$
Adj((A+I)^t)=
\begin{pmatrix}
1 & m^2 & -m \\
-m & 1 & m^2 \\
m^2 & -m & 1
\end{pmatrix}
$$

Por tanto la inversa viene dada por,

$$
(A+I)^{-1}=
\frac{\begin{pmatrix}
1 & m^2 & -m \\
-m & 1 & m^2 \\
m^2 & -m & 1
\end{pmatrix}}{m^3+1}
$$

Resolviendo la ecuación matricial tenemos,

$$
X=
\frac{\begin{pmatrix}
1 & m^2 & -m \\
-m & 1 & m^2 \\
m^2 & -m & 1
\end{pmatrix}}{m^3+1}
\cdot
\begin{pmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{pmatrix}
=
\begin{pmatrix}
\frac{1}{m^3+1} & \frac{-m}{m^3+1} & \frac{m^2}{m^3+1} \\
\frac{-m}{m^3+1} & \frac{m^2}{m^3+1} & \frac{1}{m^3+1} \\
\frac{m^2}{m^3+1} & \frac{1}{m^3+1} & \frac{-m}{m^3+1}
\end{pmatrix}
$$

Ejercicio 7. Examen de matemáticas II selectividad Junio 2023 Andalucía

El plano perpendicular al segmento de extremos \(P(0, 3, 8)\) y \(Q(2, 1, 6)\) que pasa por su punto medio corta a los ejes coordenados en los puntos \(A\), \(B\) y \(C\). Halla el área del triángulo cuyos vértices son los puntos \(A\), \(B\) y \(C\).

Dados los puntos del enunciado y sabiendo que el plano pasa por el punto medio del segmento \(PQ\) es necesario que calculemos el punto medio.

$$
M=\frac{P+Q}{2}=(1,2,7)
$$

Así podemos calcular la expresión de dicho plano ya que su vector normal coincide con el vector director \(\overrightarrow{PQ}=Q-P=(2,-2,-2)\)

$$
\pi \equiv 2x-2y-2z+D=0
$$

Como \(M\in \pi\) se debe de cumplir,

$$
2\cdot 1-2\cdot 2-2\cdot 7+D=14 \Leftrightarrow -16+D=0\Leftrightarrow D=16
$$

Por tanto el plano buscado es \( \pi \equiv 2x-2y-2z-16=0\) o equivalentemente \( \pi \equiv x-y-z-8=0\)

Haciendo la intersección con los ejes obtenemos los puntos \(A=(-8,0,0)\), \(B=(0,8,0)\) y \(C=(0,0,8)\). Podemos obtener la expresión de los vectores \(\overrightarrow{AB}=(8,8,0)\) y \(\overrightarrow{AC}=(8,0,8)\).

Sabemos que el área del triangulo se calcula como

$$
A=\dfrac{1}{2}|\overrightarrow{AB}\times \overrightarrow{AC}|
$$

El producto vectorial viene dado por,

$$
\begin{vmatrix}
i & j & k \\
8 & 8 & 0 \\
8 & 0 & 8 \\
\end{vmatrix}
=(64,-64,-64)
$$

Así el área obtenida es,

$$
A=\dfrac{1}{2}|(64,-64,-64)|=\dfrac{\sqrt{12288}}{2}=32\sqrt{3} u^2
$$

Ejercicio 8. Examen de matemáticas II selectividad Junio 2023 Andalucía

Considera el punto \(A(-1,1,3)\) y la recta \(r\) determinada por los puntos \(B=(2,1,1)\) y \(C=(0,1,-1)\)

a) Halla la distancia del punto \(A\) a la recta \(r\)

Comenzamos la recta \(r\) cuyo vector director es \(\overrightarrow{BC}=(-2,0,-2)\)

La expresión de la recta viene dada por,
$$r\equiv\left\{
\begin{align}
&x=2-2\lambda\\
&y=1\\
&z=1-2\lambda
\end{align} \right.$$
Calculamos el plano cuyo vector normal coincide con el vector director de la recta \(r\)

$$
\pi\equiv Ax+By+Cz+D=0\Rightarrow -2x-2z+D=0
$$

Imponiendo que el plano pasa por el punto \(A\) obtenemos \(D=4\) y el plano obtenido es,

$$
\pi\equiv -2x-2z+4=0 \Rightarrow \pi\equiv -x-z+2=0
$$

Calculamos ahora la intersección entre la recta y el plano simplemente sustituyendo las ecuaciones paramétricas de la recta en la expresión del plano.

$$
-(2-2\lambda)-(1-2\lambda)+2=0\Leftrightarrow \lambda=\dfrac{1}{4}
$$

Así, podemos obtener el punto de intersección sustituyendo el valor obtenido en la expresión de la recta, \(I=(\dfrac{3}{2},1,\dfrac{1}{2})\). Por tanto la distancia entre la recta y el punto \(A\) la obtenemos como el módulo del vector \(\overrightarrow{AI}\)

$$
|\overrightarrow{AI}|=|(\dfrac{5}{2},0,-\dfrac{5}{2})|=\sqrt{\left( \dfrac{5}{2}\right)^2+0^2+\left( \dfrac{5}{2}\right)^2}=\dfrac{5}{\sqrt{2}}=\dfrac{5\sqrt{2}}{2}
$$

b) Calcula el área del triángulo cuyos vertices son \( A\), \(B\), y \(C\)

Calculamos los vectores vectores \(\overrightarrow{AB}=(3,0,-2)\) y \(\overrightarrow{AC}=(1,0,-4)\).

Sabemos que el área del triangulo se calcula como

$$
A=\dfrac{1}{2}|\overrightarrow{AB}\times \overrightarrow{AC}|
$$

El producto vectorial está dado por,

$$
\begin{vmatrix}
i & j & k \\
3 & 0 & -2 \\
1 & 0 & -4 \\
\end{vmatrix}
=(0,10,0)
$$

Así el área obtenida es,

$$
A=\dfrac{1}{2}|(0,10,0)|=\dfrac{\sqrt{10^2}}{2}=5 u^2
$$

Esta es una resolución personal de los ejercicios del examen de Matemáticas II de la convocatoria de selectividad de Junio de 2023 en Andalucía (Pevau) o selectividad, por lo que otras soluciones planteadas también pueden ser válidas.

Si te ha gustado esta entrada donde resuelvo el examen de matemáticas II selectividad y quieres descubrir más material gratuito puedes visitar mi blog de matemáticas. Si te gustaría aprender más sobre matemáticas o estadística puedes visitar mi canal de Youtube donde encontrarás ejercicios de matemáticas y estadística a todos los niveles.