Examen de Matemáticas CC.SS Selectividad Junio 2021 Andalucía Resuelto

©2021 Carlos Martínez Martínez

A continuación podrás encontrar el examen de matematicas CC.SS de selectividad 2021 Andalucía resuelto paso a paso.

Si lo deseas puedes visitar mi página de exámenes de selectividad resueltos donde encontrarás exámenes de selectividad en Andalucía de distintos años resueltos paso a paso.

Ejercicio 1. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

Una empresa de recambios industriales produce dos tipos de baterías, A y B. Su producción semanal debe ser de al menos 10 baterías en total y el número de baterías de tipo B no puede superar en más de 10 unidades a las fabricadas de tipo A. Cada batería de tipo A tiene unos gastos de producción de 150 euros y cada batería de tipo B de 100 euros, disponiendo de un máximo de 6000 euros a la semana para el coste total de producción.
Si la empresa vende todo lo que produce y cada batería de tipo A genera un beneficio de 130 euros y la de tipo B de 140 euros, ¿cuántas baterías de cada tipo tendrán que producir a la semana para que el beneficio total sea máximo? ¿Cuál es ese beneficio?

Comenzamos definiendo las variables,

x=’número de baterías tipo A’
y=’número de baterías tipo B’

El sistema de inecuaciones asociado al problema es,

$$
\begin{align}
&x+y\geq 10 \\
&y\leq x+10 \\
&150x+100y\leq 6000 \\
&x \geq 0 \\
&y \geq 0
\end{align}
$$

Y la función beneficio viene dada por \(B(x,y)=130x+140y\)

La región factible junto con los vértices viene dada por,

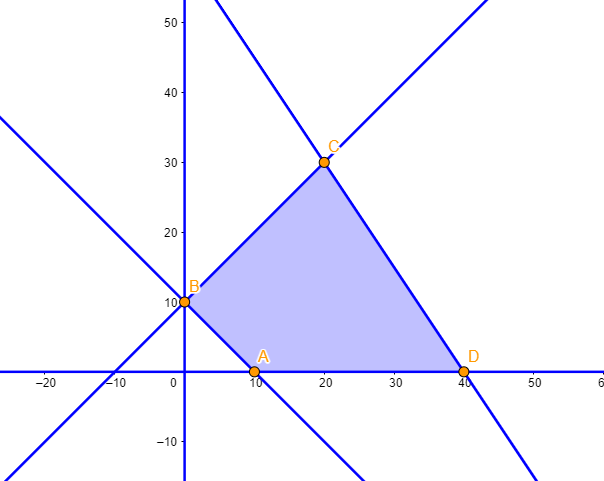
Calculando los vértices como intersección de cada pareja de rectas obtenemos,

$$
A=(10,0) \qquad B=(0,10) \qquad C=(20,30) \qquad D=(40,0)
$$

Para calcular el máximo de la función beneficio en dicho recinto evaluamos los vértices en la función obteniendo,

$$
\begin{align}
F(A)=F(10,0)=1300 \\
F(B)=F(0,10)=1400 \\
F(C)=F(20,30)=6800 \\
F(D)=F(40,0)=5200 \\
\end{align}
$$

Por tanto, el beneficio máximo se alcanza fabricando 20 baterías tipo A y 30 baterías tipo B obteniendo un beneficio de 6800€

Ejercicio 2. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

Se considera la matriz \(A=\begin{pmatrix} 1 & -1 & m \\ 0&2&-3 \\m&1&1\end{pmatrix}\), con \(m\) un parámetro real.

a) (0.7 puntos) ¿Para qué valores del parámetro \(m\) existe la matriz inversa de \(A\)?

Sabemos que existe la matriz inversa de la matriz \(A\) solamente si su determinante es distinto de 0. Por ello, vamos a ver para qué valores de \(m\) el determinante es 0 y así podremos discutir la existencia de la matriz inversa.

$$
|A|=
\begin{vmatrix}
1 & -1 & m \\
0 & 2 & -3 \\
m& 1 &1
\end{vmatrix}
=(2+3m)-(2m^2-3)=0\Leftrightarrow -2m^2+3m+5=0\Leftrightarrow m=-1 \quad \text{y} \quad m=\dfrac{5}{2}
$$

Podemos afirmar que, para \(m\neq -1\) y \(m \neq \dfrac{5}{2}\), el determinante de \(A\) es distinto de 0 y por tanto existe la matriz inversa de \(A\)

b) (1.8 puntos) Para \(m=2\), resuelva la ecuación matricial \(X\cdot A-A^2=I_3\).

Comenzamos resolviendo de forma teórica la ecuación matricial,

$$
\begin{align}
X\cdot A-A^2=I_3 &\Leftrightarrow X \cdot A= I_3+A^2 \\
&\Leftrightarrow X\cdot A\cdot A^{-1}=(I_3+A^2)\cdot A^{-1} \\
&\Leftrightarrow X=A^{-1}+A
\end{align}
$$

Calculamos la expresión de \(A^{-1}\) utilizando que,

$$
A^{-1}=\dfrac{\text{Adj}(A^t)}{|A|}
$$

Para \(m=2\) la matriz \(A\) viene dada por \(A=\begin{pmatrix} 1 & -1 & 2 \\ 0 & 2 & -3 \\ 2& 1 &1 \end{pmatrix}\).

Del apartado anterior sabemos que \(|A|=-2m^2+3m+5\), sustituyendo \(m=2\) tenemos \(|A|=3\).

Por otra parte,

$$
A^t=
\begin{pmatrix}
1 & 0 & 2 \\
-1 & 2 & 1 \\
2 & -3 & 1
\end{pmatrix}
\Rightarrow
\text{Adj}(A^t)=
\begin{pmatrix}
5 & 3 & -1 \\
-6 & -3 & 3 \\
-4& -3 & 2
\end{pmatrix}
$$

Obtenemos,

$$
A^{-1}=\dfrac{\begin{pmatrix}5 & 3 & -1 \\-6 & -3 & 3 \\-4& -3 & 2\end{pmatrix}}{3}=\begin{pmatrix}
\dfrac{5}{3} & 1 & -\dfrac{1}{3} \\
-2 & -1 & 1 \\
-\dfrac{4}{3} & -1 & \dfrac{2}{3}
\end{pmatrix}
$$

Resolvemos la ecuación matricial obteniendo,

$$
X=A^{-1}+A=
\begin{pmatrix}
\dfrac{5}{3} & 1 & -\dfrac{1}{3} \\
-2 & -1 & 1 \\
-\dfrac{4}{3} & -1 & \dfrac{2}{3}
\end{pmatrix}
+
\begin{pmatrix}
1 & -1 & 2 \\
0 & 2 & -3 \\
2& 1 &1
\end{pmatrix}
=
\begin{pmatrix}
\dfrac{8}{3} & 0 & \dfrac{5}{3} \\
-2 & 1 & -2 \\
\dfrac{2}{3} & 0 & \dfrac{5}{3} \end{pmatrix}
$$

Ejercicio 3. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

Se considera la función \(f(x)=x^3-4x^2+4x\).

a) (1 punto) Estudie su monotonía y calcule sus extremos.

Para estudiar la montonía comenzamos calculando la derivada de la función \(f\) y la igualamos a 0.

$$
f'(x)=3x^2-8x+4=0\Leftrightarrow x=2\quad \text{y} \quad x=\dfrac{2}{3}
$$

Podemos afirmar que,

• En \((-\infty,\dfrac{2}{3}), \, f'(x)>0 \Rightarrow f\) es creciente
• En \((\dfrac{2}{3},2,) \, f'(x)<0 \Rightarrow f\) es decreciente
• En \((2,\infty), \, f'(x)>0 \Rightarrow f\) es creciente

Como consecuencia del estudio de la monotonía podemos afirmar que en \(x=\dfrac{2}{3}\) existe un máximo relativo y sus coordenadas son \(\left( \dfrac{2}{3}, f\left(\dfrac{2}{3} \right)\right)=\left( \dfrac{2}{3} ,\dfrac{32}{27}\right) \)

Por otra parte, en \(x=2\) existe un mínimo relativo y sus coordenadas son \( (2,f(2))=(2,0)\)

b) (0.5 puntos) Represente gráficamente la función

Para representar la función usamos la información obtenida en el apartado anterior y si fuera necesario realizaríamos una tabla de valores para obtener algunos puntos más de la función. Obtenemos entonces,

c) (0.5 puntos) Calcule \(\int f(x)dx\)

$$
\int x^3-4x^2+4x dx=\dfrac{x^4}{4}-\dfrac{4x^3}{3}+2x^2+C
$$

d) (0.5 puntos) Calcule el área del recinto acotado limitado por la gráfica de \(f\) y el eje de abscisas.

Para calcular el área del recinto limitado por la gráfica de la función y el eje de abscisas solo tenemos que resolver,

$$
\int_0^2f(x)dx=\left[\dfrac{x^4}{4}-\dfrac{4x^3}{3}+2x^2 \right]_0^2=\left( \dfrac{16}{4}-\dfrac{32}{3}+8\right)-(0)=\dfrac{4}{3} \, u^2
$$

Ejercicio 4. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

a) (1 punto) Calcule la derivada de las siguientes funciones

$$
f(x)=\ln \left( \dfrac{x-1}{x+1}\right) \qquad g(x)=x^3\cdot e^{2x^2}
$$

Para calcular la derivada de la función \(f\) utilizamos la regla de derivación de logaritmo junto con la derivada de un cociente al aplicar la regla de la cadena,

$$
f'(x)=\dfrac{\dfrac{(x+1)-(x-1)}{(x+1)^2}}{\dfrac{x-1}{x+1}}=\dfrac{\dfrac{2}{(x+1)^2}}{\dfrac{x-1}{x+1}}=\dfrac{2}{(x+1)(x-1)}=\dfrac{2}{x^2-1}
$$

Para calcular la derivada de la función \(g\) utilizamos la regla de derivación de un producto junto con la derivada de una función exponencial para poder aplicar la regla de la cadena,

$$
g'(x)=3x^2\cdot e^{2x^2}+x^3\cdot 4xe^{2x^2}=e^{2x^2}(3x^2+4x^4)
$$

b) (0.7 puntos) Represente gráficamente la parábola \(h(x)=x^2+x+1\), indicando el vértice y los puntos de corte con los ejes coordenados.

Calculamos los puntos de corte con los ejes. En primer lugar imponemos \(h(x)=0\) para calcular los puntos de corte con el eje x, por tanto tenemos que resolver la ecuación,

$$
x^2+x+1=0
$$

La cual no tiene solución por lo que no existen puntos de corte con el eje x. Para calcular el punto de corte con el eje y imponemos \(x=0=\) obteniendo \( y=1\). Por tanto la parábola corta al eje en el punto de coordenadas \((0,1)\).

Sabemos que el vértice se calcula como \(V=\left(\dfrac{-b}{2a},h\left( \dfrac{-b}{2a}\right) \right)\). Obteniendo,

$$
\dfrac{-b}{2a}=-\dfrac{1}{2} \quad \text{y}\quad h\left( -\dfrac{1}{2}\right)=\dfrac{3}{4}
$$

Y la función buscada es,

c) (0.8 puntos) Calcule el área del recinto limitado por la gráfica de \(h(x)=x^2+x+1\), el eje de abscisas y las rectas \(x=-\dfrac{1}{2}\) y \(x=0\)

El área pedida se obtiene sin más que resolver la integral,

$$
\int_{-1/2}^0 x^2+x+1 dx=\left[ \dfrac{x^3}{3}+\dfrac{x^2}{2}+x\right]_{-1/2}^0=\dfrac{5}{12}\, u^2
$$

Ejercicio 5. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

Se desea probar la eficacia de dos tipos de vacunas, A y B, contra un virus determinado. Para ello, se seleccionan 5000 voluntarios sin anticuerpos para este virus, a los que se les administra una de las vacunas o un placebo, resultando que 3000 reciben la vacuna A, 1500 la B y el resto el placebo. Se comprueba que el 90% de los vacunados con la A y el 95% de los vacunados con la B, generan anticuerpos, no generando anticuerpos los que han recibido el placebo. Se selecciona uno de esos voluntarios al azar.

a) (1.5 puntos) ¿Cuál es la probabilidad de que haya generado anticuerpos?

Comenzamos este ejercicio definiendo los siguientes sucesos.

• A=’Ser vacunado con la vacuna tipo A’
• B=’Ser vacunado con la vacuna tipo B’
• Pl=’Recibir placebo’
• G=’Generar anticuerpos’

A partir de los datos del enunciado podemos obtener las siguientes probabilidades representadas en un diagrama de árbol

Para calcular la probabilidad pedida utilizaremos el Teorema de la Probabilidad Total,

$$
P(G)=P(A)\cdot P(G/A)+P(B)\cdot P(G/B)=0’6\cdot 0’9+0’3\cdot 0’95=0’825
$$

b) (1 punto) Si dicho voluntario no ha generado anticuerpos, ¿qué probabilidad hay de que se le haya administrado placebo?

Para resolver este apartado utilizamos el Teorema de Bayes,

$$
P(Pl/\overline{G})=\dfrac{P(Pl)\cdot P(\overline{G}/Pl)}{P(\overline{G})}=\dfrac{P(Pl)\cdot P(\overline{G}/Pl)}{1-P(G)}=\dfrac{0’1\cdot 1}{1-0’825}=0’571
$$

Ejercicio 6. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

De las compras realizadas en el último periodo de rebajas del pasado año, el 55% se dedicaron a productos electrónicos, el 72% se hicieron a través de internet y, de las compras que se hicieron por internet, el 64% fueron de productos electrónicos. Se elige una compra al azar.

a) (1 punto) Calcule la probabilidad de que haya sido de productos electrónicos y se haya realizado por internet.

Para realizar este ejercicio comenzamos definiendo los siguientes sucesos,

• E=’Comprar productos electrónicos’
• I=’Comprar a través de internet’

Por el enunciado sabemos que,

$$
P(E)=0’55 \quad P(I)=0’72 \quad P(E/I)=0’64
$$

Nos piden que calculemos \(P(E\cap I)\). Utilizando la definición de probabilidad condicionada y los datos del enunciado tenemos,

$$
P(E/I)=\dfrac{P(E\cap I)}{P(I)}\Leftrightarrow 0’64=\dfrac{P(E\cap I)}{0’72}\Leftrightarrow P(E\cap I)=0’64\cdot 0’72=0’4608
$$

b) (0.75 puntos) Calcule la probabilidad de que la compra se haya realizado por internet o que se hayan comprado productos electrónicos.

En esta ocasión nos piden que calculemos \(P(I\cup E)\). Aplicando la probabilidad de la unión tenemos,

$$
P(I\cup E)=P(I)+P(E)-P(I\cap E)=0’72+0’55-0’4608=0’8092
$$

c) (0.75 puntos) Calcule la probabilidad de que sabiendo que no se compraron productos electrónicos, la compra no se hiciera a través de internet.

Aquí debemos calcular \(P(\overline{I}/\overline{E})\). Para ello usamos la definición de probabilidad condicionada junto con las leyes de Morgan,

$$
P(\overline{I}/\overline{E})=\dfrac{P(\overline{I}\cap\overline{E})}{P(\overline{E}}=\dfrac{P(\overline{I\cup E})}{1-P(E)}=\dfrac{1-P(I\cup E)}{1-P(E)}=\dfrac{1-0’8092}{1-0’55}=0’424
$$

Ejercicio 7. Examen de matemáticas CC.SS selectividad Junio 2021 Andalucía

a) (1.5 puntos) En una Escuela Politécnica hay matriculados en el último curso 60 estudiantes de Ingeniería Eléctrica, 40 de Ingeniería Informática, 30 de Ingeniería Civil, 50 de Ingeniería Mecánica y 20 de Ingeniería Aeronáutica. Se quiere hacer una encuestas al 20% de estos estudiantes, de manera proporcional al número de matriculados en cada titulación.

1. ¿Qué tipo de muestreo se debe emplear?

Para realizar un muestreo de manera proporcional lo más adecuado es realizar un muestreo aleatorio estratificado con afijación proporcional.

2. ¿Cuántos alumnos debe haber en la muestra y cuántos de cada titulación?

En esta ocasión tenemos un total de \(N=60+40+30+50+20=200\) alumnos. Como queremos hacer una muestra al 20% de los estudiantes obtenemos que \(n=40\) alumnos.

Además sabemos que \(N_1=60\), \(N_2=40\), \(N_3=30\), \(N_4=50\) y \(N_5=20\),

Como estamos ante un muestreo aleatorio estratificado se ha de verificar que,

$$
\dfrac{n}{N}=\dfrac{n_1}{N_1}=\dfrac{n_2}{N_2}=\dfrac{n_3}{N_3}=\dfrac{n_4}{N_4}=\dfrac{n_5}{N_5}
$$

Utilizando los datos del enunciado obtenemos,

$$
\begin{align}
&\dfrac{40}{200}=\dfrac{n_1}{60}\Leftrightarrow n_1=\dfrac{40\cdot 60}{200}=12 \\ \\
&\dfrac{40}{200}=\dfrac{n_2}{40}\Leftrightarrow n_1=\dfrac{40\cdot 40}{200}=8 \\ \\
&\dfrac{40}{200}=\dfrac{n_3}{30}\Leftrightarrow n_4=\dfrac{40\cdot 30}{200}=6 \\ \\
&\dfrac{40}{200}=\dfrac{n_4}{50}\Leftrightarrow n_1=\dfrac{40\cdot 50}{200}=10 \\ \\
&\dfrac{40}{200}=\dfrac{n_5}{20}\Leftrightarrow n_1=\dfrac{40\cdot 20}{200}=4 \\ \\
\end{align}
$$

Por tanto la muestra está compuesta por,

• 12 Alumnos de Ingeniería Eléctrica
• 8 Alumnos de Ingeniería Informática
• 6 Alumnos de Ingeniería Civil
• 10 Alumnos de Ingeniería Mecánica
• 4 Alumnos de Ingeniería Aeronáutica

b) (1 punto) Dada la población \(\{ a,\,10,\,12,\,11,\,18\}\),¿cuánto debe valer \(a\), sabiendo que la media de las medias muestrales de tamaño 3, obtenidas mediante muestreo aleatorio simple es 13.2?

En esta ocasión tenemos que utilizar la media de las medias muestrales coincide con la media poblacional, es decir,

$$
13’2=\dfrac{a+10+12+11+18}{3}\Leftrightarrow 66=a+51\Leftrightarrow a=15
$$

Ejercicio 8. Examen de matemáticas CCSS selectividad Junio 2021 Andalucía

Se desea estimar la proporción de individuos mayores de edad de una localidad que están en contra de la construcción de una central nuclear en su término municipal. Para ellos, se pregunta a 100 individuos mayores de edad de esa localidad, elegidos de forma aleatoria, resultando que 45 de ellos rechazan la construcción de la central.

a) Calcule un intervalo de confianza al 92% para estimar la proporción real de individuos de esa localidad que están en contra de la construcción de la central.

Sabemos que el intervalo de confianza para la proporción de individuos que están en contra de la construcción de la central nuclear viene dado por,

$$
\left( p-z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}, p+z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} \right)
$$

donde \(p\) es la proporción de individuos de la muestra que está en contra de la construcción de la central nuclear. Luego \(p=45/100=0’45\)

Sabemos que el nivel de confianza es del 92% luego,

$$
0’92=1-\alpha\Rightarrow \alpha=0’08
$$

A continuación, buscamos un valor \(z_{\alpha /2}\) tal que,

$$
P(Z < z_{\alpha/2})=1-\frac{\alpha}{2}=0’96
$$

Y buscamos en la tabla de frecuencias de la distribución N⁡(0,1), el valor con una probabilidad asociada de 0’96. Observando la tabla vemos que el valor 1’75 tiene una probabilidad 0′⁢9599 mientras que el valor 1’76 tiene una probabilidad 0′⁢9608. Como buscamos el valor que de una probabilidad 0′⁢96 tomamos el punto medio de 1’75 y 1’76, esto es,

$$
z_{\alpha /2}=1’755
$$

Sustituyendo en la expresión del intervalo de confianza tenemos,

$$
\begin{align*} IC&= \left( 0’45-1’755\sqrt{\frac{0’45(1-0’45)}{100}}, 0’45+1’755\sqrt{\frac{0’45(1-0’45)}{100}} \right) \\ \\ &= \left( 0’3627,0’5373 \right) \end{align*}
$$

b) Suponiendo que se mantiene la misma proporción muestral y el mismo nivel de confianza del apartado anterior, determine el tamaño mínimo de la muestra que hay que tomar, para que al estimar la proporción de individuos de esa localidad que rechazan la construcción de la central, el error cometido sea inferior al 5%.

El error cometido viene dado por,

$$
E=z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}
$$

Como el nivel de confianza y la proporción de individuos es la misma que en el apartado anterior tenemos,

$$
\begin{align} 0’05=1’755\sqrt{\frac{0’45(1-0’45)}{n}}&\Leftrightarrow 0’05 =1’755\frac{\sqrt{0’45(1-0’45)}}{\sqrt{n}} \\ \\ &\Leftrightarrow \sqrt{n}=1’755\frac{\sqrt{0’45(1-0’45)}}{0’05} \\ \\ &\Leftrightarrow n=304’95 \end{align}
$$

Si queremos garantizar que el error cometido sea menor que 0’05 habrá que aumentar el tamaño de la muestra y por tanto redondear el valor de n a \(n=305\)

Esta es una resolución personal de todos los ejercicios del examen de matemáticas CC.SS de la convocatoria de selectividad de Junio de 2021 en Andalucía (Pevau) por lo que otras soluciones planteadas también pueden ser válidas.

Si te ha gustado esta entrada con la resolución del examen de matemáticas CC.SS selectividad y quieres descubrir más material gratuito puedes visitar mi blog de matemáticas. Si te gustaría aprender más sobre matemáticas o estadística puedes visitar mi canal de Youtube donde encontrarás ejercicios resueltos de matemáticas y estadística a todos los niveles.